Barisan dan Deret Aritmetika

1. Pola Bilangan

Sekumpulan bilangan yang adakalanya mengikuti pola tertentu. Pola ini sering digunakan dalam menentukan urutan atau letak bilangan dari sekumpulan bilangan yang telah ditentukan. Pola bilangan dapat berupa gambar, formula, atau rumus untuk menentukan nilai bilangan berdasarkan urutannya. Pola bilangan yang disusun berdasarkan urutan tertentu disebut barisan bilangan. Jadi, barisan bilangan merupakan susunan anggota suatu himpunan bilangan yang diurutkan berdasarkan pola atau aturan tertentu. Anggota barisan bilangan disebut suku barisan yang dituliskan sebagai π‘ˆπ‘› yaitu:

π‘ˆ1 ,π‘ˆ2 ,π‘ˆ3 , . . . , π‘ˆπ‘›

Ket:

π‘ˆ1 merupakan Suku Pertama

π‘ˆ2 merupakan Suku Kedua

π‘ˆ3 merupakan Suku Ketiga

π‘ˆπ‘› merupakan Suku ke-n

Barisan bilangan memiliki rumus atau formula sesuai aturan tertentu. Berikut ini beberapa contoh barisan bilangan dengan rumus formulanya:

a) Pola barisan bilangan asli

Barisan Bilangan : 1, 2, 3, 4, 5, . . . , π‘ˆπ‘›

Rumus Suku ke-n : π‘ˆπ‘› = 𝑛

b) Pola barisan bilangan cacah

Barisan Bilangan : 0, 1, 2, 3, 4, . . ., π‘ˆπ‘›

Rumus Suku ke-n : π‘ˆπ‘› = 𝑛 βˆ’ 1

c) Pola barisan bilangan ganjil

Barisan Bilangan : 1, 3, 5, 7, . . ., π‘ˆπ‘›

Rumus Suku ke-n : π‘ˆπ‘› = 2𝑛 βˆ’ 1

d) Pola barisan bilangan genap

Barisan Bilangan : 2, 4, 6, 8, . . ., π‘ˆπ‘›

Rumus Suku ke-n : ⡐𝑛 = 2𝑛

e) Pola barisan bilangan segitiga

Barisan Bilangan : 1, 3, 6, 10, . . ., π‘ˆπ‘›

Rumus Suku ke-n : π‘ˆπ‘› = 𝑛(𝑛 + 1)

f) Pola barisan bilangan persegi

Barisan Bilangan : 1, 4, 9, 16, . . . , π‘ˆπ‘›

Rumus Suku ke-n : π‘ˆπ‘› = 𝑛

g) Pola barisan bilangan persegi panjang

Barisan Bilangan : 2, 6, 12, 20, . . . , π‘ˆπ‘›

Rumus Suku ke-n : π‘ˆπ‘› = 𝑛(𝑛 + 1)

Penjumlahan dari suku-suku bilangan disebut deret. Bentuk umum deret bilangan adalah: π‘ˆ1 + π‘ˆ2 + π‘ˆ3 + . . . + π‘ˆπ‘›.

Menurut banyak suku-suku pembentuknya, deret bilangan dibedakan menjadi dua, yaitu:

a) Deret berhingga, contohnya: 1 + 3 + 5 + 7 + 9 + 11 + 13

b) Deret tak hingga, contohnya: 1 + 3 + 5 + 7 + 9 + … .

2. Barisan Aritmetika

Barisan Aritmatika merupakan barisan bilangan dengan pola tertntentu dimana suku-suku pada barisan yang berurutan mempunyai selisih yang selalu tetap (konstan). Contoh barisan bilangan: 2, 5, 8, 11, 14, 17, . . . . +3 +3 +3 +3 +3 Dari bilangan pertama ke bilangan kedua ditambah 3, dari bilangan kedua ke bilanga ketiga ditambah 3, dari bilangan ketiga ke bilangan keempat ditambah 3. Penambahan (selisih) antara dua bilangan yang berurutan seperti itulah yang disebut sebagai barisan aritmatika. Dari contoh tersebut, suku pertama dinotasikan a = 2, selisih/ beda dinotasikan b = 3, suku kedua dituliskan π‘ˆ2 = 5, suku ketiga dituliskan π‘ˆ3 = 8, dan suku barisan ke-n dituliskan π‘ˆπ‘› .

Rumus Barisan Aritmatika

Jika suku pertama (π‘ˆ1 ) dinyatakan dengan a, selisih (beda) antara dua suku yang berurutan ditulis dengan notasi b, dan suku barisan ke-n dinyatakan dengan π‘ˆπ‘› , maka barisan bilangan artimatika dituliskan sebagai berikut: π‘Ž, π‘Ž + 𝑏, π‘Ž + 2𝑏, π‘Ž + 3𝑏, . . . , π‘ˆπ‘›

Bentuk Umum:

π‘ˆ1 = π‘Ž = π‘Ž + 0. 𝑏 = π‘Ž 1 βˆ’ 1 𝑏

π‘ˆ2 = π‘ˆ1 + 𝑏 = π‘Ž + 𝑏 = π‘Ž + 1. 𝑏 = π‘Ž (2 – 1) 𝑏

π‘ˆ3 = π‘ˆ2 + 𝑏 = ( π‘Ž + 𝑏 ) + 𝑏 = π‘Ž + 2. 𝑏 = π‘Ž (3 – 1)b

Contoh Soal

1.Rumus suku ke-n barisan aritmatika: 3, 5, 7, 9, … adalah … .

  1. Nilai π‘ˆ7 dari barisan -2, 1, 4, 7, … adalah … .
  2. Dari suatu barisan aritmatika diketahui π‘ˆ2 = 7 dan π‘ˆ5 = 19, nilai suku ke-10 adalah … . 4. Suatu peternakan ayam petelur menghasilkan telur yang bertambah 5 butir setiap harinya. Jika pada hari senin telur yang diperoleh 15 butir, maka jumlah telur yang diperoleh peternak pada hari Jumat ada … butir.

Penyelesaian:

  1. Suku Pertama a = 3; beda b = 5 – 3 = 2

𝑼𝒏 = 𝒂 + (𝒏 βˆ’ 𝟏 )𝒃 = πŸ‘ + (𝒏 βˆ’ 𝟏 )𝟐 = πŸ‘ + πŸπ’ βˆ’ 𝟐 = πŸπ’ + πŸ‘ βˆ’ 𝟐 = πŸπ’ + 𝟏

Jadi Rumus barisan tersebut adalah 𝑼𝒏 = πŸπ’ + 1

  1. a = -2; b = 1 – (-2) = 1 + 2 = 3;

yang ditanyakan U7 maka n = 7

𝑼𝒏 = 𝒂 + (𝒏 – 𝟏) 𝒃

π‘ΌπŸ• = βˆ’πŸ + πŸ• βˆ’ 𝟏 πŸ‘ = βˆ’πŸ + πŸ”. πŸ‘ = βˆ’πŸ + πŸπŸ– = πŸπŸ”

Jadi nilai π‘ΌπŸ• = 16

4. Dari soal cerita, diketahui b = 5, a =15
Ditanyakan: jumlah telur hari jumat, maka U5 = … .
π‘ˆ5 = π‘Ž + 𝑛 βˆ’ 1 𝑏
= 15 + 5 βˆ’ 1 5
= 15 + 4.5

= 15 + 20 = 35
Jadi jumlah telur peternak pada hari Jumat adalah 35 butir

3. Deret Aritmatika
Suatu Deret bilangan dengan pola tertentu dengan selisih antara dua suku yang berurutan
selalu tetap disebut Deret Aritmatika. Jadi Deret aritmetika adalah suatu deret yang diperoleh
dari menjumlahkan suku-suku pada barisan aritmetika.
Dari barisan aritmetika: U1, U2, U3, U4, … … …, Un.
Dapat dibentuk deret aritmetika: U1 + U2 + U3 + U4 + … … … + U10

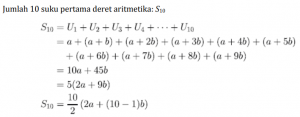
4. Masalah kontekstual yang berkaitan dengan Barisan dan Deret Aritmetika

Masalah sehari-hari yang merupakan penerapan dari barisan dan deret aritmetika umumnya tidak selesai sampai nilai masing-masing variabel ditemukan. Diperlukan interpretasi lebih lanjut agar nilai variabel yang ditemukan dapat menjawab pertanyaan. Secara umum urutan penyelesaian permasalahan barisan dan deret Aritmetika terdiri atas lima langkah, yakni :

  1. Menganalisis teks;
  2. Mengidentifikasi jenis barisan;
  3. Mengubah pernyataan verbal ke dalam model matematika;
  4. Menyelesaikan model matematika;
  5. Melakukan interpretasi hasil sesuai pernyataan.

sumber :

Ediyanto & Harsasi. 2021. Buku Matematika untuk SMK/MAK Kelas X. Jakarta : Erlangga.

thttps://files1.simpkb.id/guruberbagi/rpp/447102-1638709222.pdf